Bohr Model of Hydrogen Atom Equation

Bohr Model of the hydrogen atom initially projected the planetary model, but later an assumption regarding the electrons was made. The assumption made was the quantization of the structure of atoms. Bohr’s projected that electrons revolved around the nucleus in specific paths termed as orbits or shells with a fixed radius.

Scientifically, the value of the atomic radius is given by the equation as follows:

r(n)=n²×r(1)

Where,

• n represents a positive integer

• r(1) represents the smallest allowed radius for the hydrogen atom also called as Bohr’s radius

Planetary Model of the Atom

Quantum mechanics arose in the mid-1920s. Neil Bohr, one of the founders of quantum mechanics, was involved in the much-debated topic of that time which is the structure of an atom. Several atomic models, including the theory proposed by J.J Thompson and the finding of a nucleus by Ernest Rutherford, had arisen over time. But Neil Bohr proposed the planetary model, which stated that electrons revolve around a positively charged nucleus just like the planets orbit around the sun.

Bohr Model of Hydrogen Atom

Bohr’s model of the hydrogen atom initially started from the planetary model, but he further added one assumption concerning the electrons. Bohr proposed that the electrons present in an atom could only orbit the nucleus in definite orbits or shells with a fixed radius.

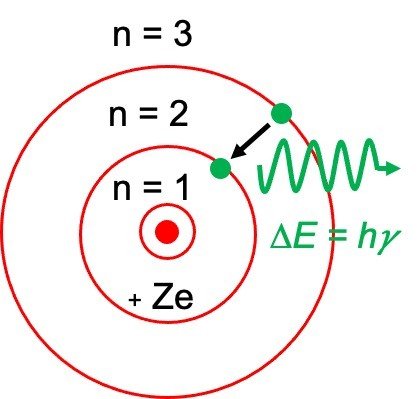
By considering the electrons in circular, quantized orbits revolving around the positively charged nucleus, Bohr also determined the energy of an electron.

Absorption and Emission

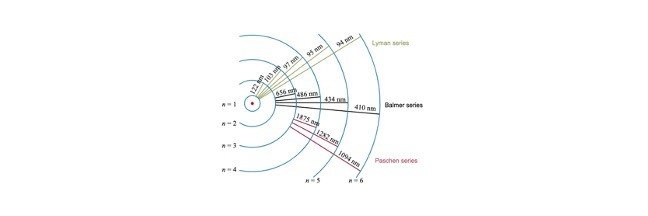
The energy level diagram shown below displays transitions for the Balmer series, it has the n=2 energy level as the ground state.

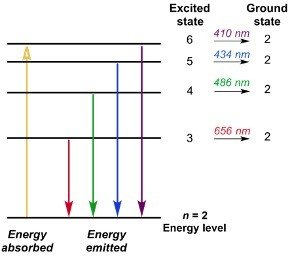
Bohr was successful in describing the processes of absorption and emission of electrons. According to Bohr’s model, an electron generally absorbs energy in the form of photons to get excited to a higher state. This higher energy level is also known as the excited state. After reaching the higher energy level the excited electron would be in a less stable state, and consequently, the electron would quickly emit a photon and will be back to its lower, more stable energy state.

The energy of the emitted photon is thus equal to the difference in two energy levels for a definite transition.

The energy can be determined by using the equation given below;

hν = z²me⁴/8h²ε₀² [(1/n₁²) – (1/n₂²)]

= -13.6z² [(1/n₁²) – (1/n₂²)]eV

Bohr Model of Hydrogen Atom: Some Important Equations

The equation to find the Radii of Bohr’s stationary orbits is as follows;

r_n = n²(h²ε_o/πmZe²)

• n represents integer

• r_n represents the radius of the nth orbit

• h represents Planck’s constant

• ε_o represents the Electric constant

• m represents the mass of the electron

• Z represents the Atomic number of the atom

• e represents Elementary charge

The equation to find the velocity of Electron in Bohr’s Stationary is;

v_n = (Ze²/2hε_o) (1/n)

Since ε_o, h, and e are the constants and for a hydrogen atom, Z or atomic number is equal to 1

Hence,

r_n α (1/n)

Total Energy of Electron in Bohr’s Stationary Orbits is given by;

E_n = -(me⁴/8ε_o²h²)(Z²/n²) or

E_n = -13.6 (Z²/n²) eV

The negative sign signifies that the electron is bound to the nucleus. The energy thus obtained is always a negative number.

However, these equations were derived by assuming that the electron revolves around the nucleus in a circular path, further experiments directed by Arnold Sommerfeld stated that these equations are applicable even for elliptical orbits.

Energy Levels

The minimum energy required to release an electron from the ground state of an atom is equal to 13.6 eV. This energy is termed as the ‘Ionization Energy’ of the hydrogen atom.

E₁ = -13.6 eV

A hydrogen atom is generally present in the ‘Ground State’ at room temperature. The atom might take energy from various processes such as electron collision and thus gains enough energy to move the electron to higher energy states or orbits. This is termed as the ‘excited’ state of the atom. Hence, the energy that is required by the atom to excite an electron is as follows;

E₂ – E₁ = -3.40 eV – (-13.6) eV = 10.2 eV

Correspondingly, the energy required to excite the electron to its second excited state is as follows:

E₃ – E₁ = -1.51 eV – (-13.6) eV = 12.09 eV

Bohr model of the hydrogen atom was the first atomic model to effectively describe the radiation spectra of atomic hydrogen. Niel Bohr presented the atomic Hydrogen model in the year 1913. Bohr’s model of atom holds a distinct place in the past as it gave rise to quantum mechanics by proposing the quantum theory.

Limitations of the Bohr Model of Hydrogen Atom

• Bohr’s model explained the structure of simple atoms such as hydrogen but failed to explain the structure for complex atoms.

• Bohr was unable to explain that why some spectral lines are more intense than others.

• Heisenberg’s uncertainty principle opposes Bohr’s idea of electrons. According to Bohr’s model of the atom, an electron present in an atom is positioned at a fixed distance from the nucleus and is revolving with a definite velocity around the positively charged nucleus.

But Heisenberg’s uncertainty principle states that it is nearly impossible to determine the exact position and velocity (or momentum) of the electron at the same time.

The Bohr model helped in explaining the structure of hydrogen atom and other single-electron structures. Unfortunately, he was unable to explain the spectra of more complex atoms. Moreover, the Bohr model failed to explain why some lines are more intense as compared to other lines or why some spectral lines split into several lines in the presence of a magnetic field. This phenomenon of splitting of spectral lines in presence of a magnetic field is termed as Zeeman effect.

In the following decades, the theories proposed by different scientists such as Erwin Schrödinger presented that electrons can be assumed to behave like waves as well as particles. This further means that it is not possible to know an electron’s location in space and its velocity at the same time, a concept that is stated in Heisenberg’s uncertainty principle.