Electron Transport Chain (ETC)

Electron Transport Chain (ETC) is an aerobic, occurs across the inner cell membrane for prokaryotes, inner mitochondrial membrane for eukaryotes.

Structure of Electron Transport Chain (ETC)

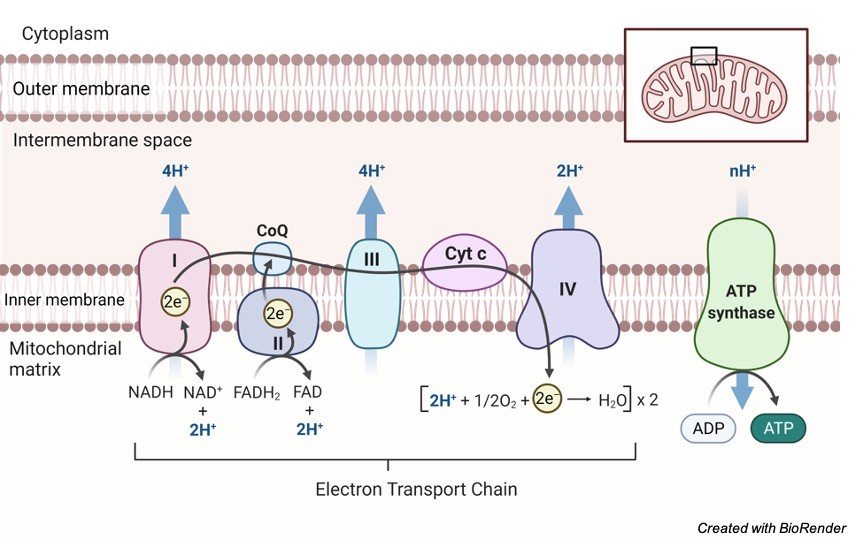
• Oxidative phosphorylation oxidizes NADH to NAD+, which creates a proton gradiant, via the pumping out of H+, that propels protons through ATP synthase.

• So the intermembrane space has a lower pH/higher [H+ concentration] than the matrix.

• The inter-cristal space or the mitochondrial matrix has a low H+ concentration and a high pH.

• NADH oxidation back to NAD and FADH2 oxidation back to FAD occur along with ATP production, allowing the earlier stages to continue.

• As electrons move within the ETC each intermediate carrier is reduced by the preceding molecule and oxidized by the following

• Oxygen is the last electron acceptor in the ETC

• 1 NADH produces 3 ATP molecules

• 1 FADH produces 2 ATP molecules

Electron Transport Chain (ETC) Summary

• 36 net ATP produced in eukaryotes, 38 net ATP produced in prokaryotes (because the electrons from the NADH produced from pyruvate decarboxylation do not have to be transported across the mitochondrial membrane in prokaryotes; doing this causes a net loss of two ATP in eukaryotes)

• Products and Reactants for Respiration:

Glucose + O2 → CO2 + H2O